On Wednesday, June 30th, HNR+ResHist2021 will offer four workshops for beginners as well as advanced network researchers:
- Analysis of Two-Mode Networks with Python
Demival Vasques Filho - Exponential Random Graph Models: Theory and Applications on Historical Networks
Antonio Fiscarelli - From historical source to network data
Claire Lemercier - Introduction to Social Network Analysis: Basics and Historical Specificities
Martin Grandjean
For more information regarding times and rooms, please check the conference programme.
Unfortunately, the workshops are completely booked out. For those who won’t be able to join, we will post the videos of the workshops on the HNR YouTube Channel after the conference.
Analysis of Two-Mode Networks with Python
Demival Vasques Filho
Leibniz-Institut fur Europäische Geschichte, 55116 Mainz, Germany
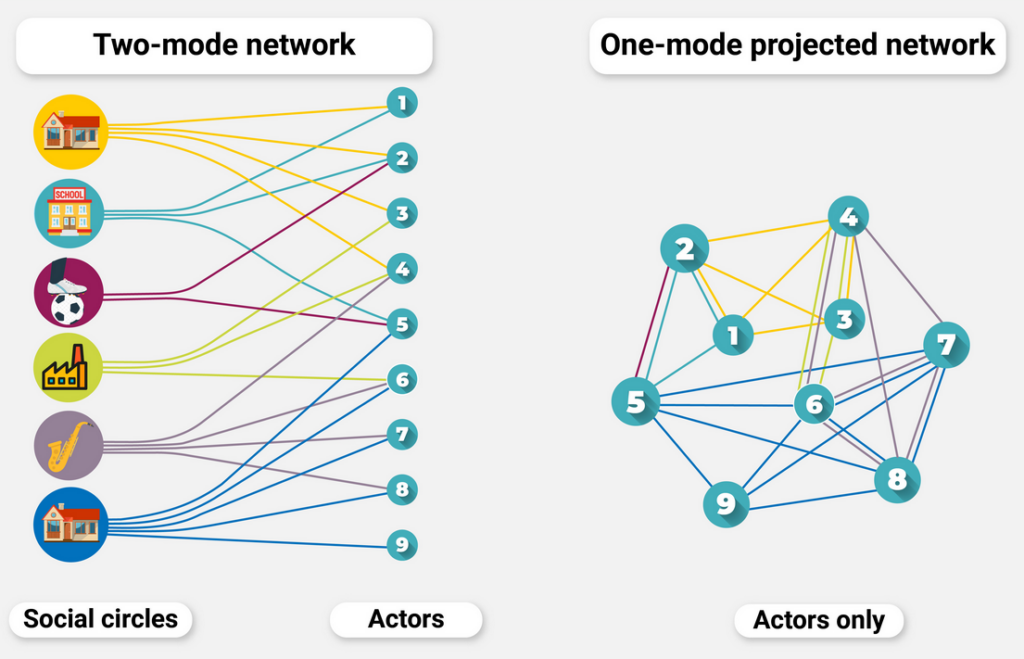
Many systems represented by networks are projections of more complicated structures. Often, the original network has a bipartite architecture comprised of two different types of nodes; thus the name two-mode (or bipartite) networks. Examples are relations based on membership, affiliation, collaboration, employment, ownership, and others.
We use (one-mode) projections of two-mode networks mainly for two reasons. First, we are often more interested in only one of the types of nodes; those with agency. Second, there is a myriad of metrics for studying one-mode networks, while there exist fewer well-established one to characterize the structural properties of a two-mode network.
In this workshop, we will learn about the metrics that we employ to directly analyze two-mode networks as, for instance, the degree distribution of both sets of nodes, redundancy, clustering coefficients, and the presence of motifs (small-cycles). Also, we will discuss projections, and how and when to use the different methods for creating one-mode projected networks, such as simple, multi, and weighted graph projections.
We highly suggest that all attendees have the Anaconda Distribution already installed on their computers. Anaconda provides Python, Jupyter Notebook, and all the Python libraries that we will use during the workshop.
Participants do not need to have previous knowledge of two-mode networks or Python. Nevertheless, it is helpful to have some familiarity with networks in general, and with the programming language, before attending the workshop.
Exponential Random Graph Models: Theory and Applications on Historical Networks
Antonio Maria Fiscarelli1 [0000-0003-0287-4388]
Supported by the Luxembourg National Research Fund (FNR) DTU-DHH, C2DH, CSC-ILIAS, University of Luxembourg, 11, Porte des Sciences, L-4366 Esch-sur-Alzette, Luxembourg
This workshop will provide an introduction to Exponential Random Graph Mod els (ERGMs), followed by some example applications on historical networks. ERGMs are a family of statistical models that help discover the processes underlying network formation [1–3]. They have been used extensively in social network analysis and are popular in various fields such as sociology [4, 5], ar chaeology [6], and history [7]. Within this framework, one can:
- Define a model for a network that includes covariates representing features like homophily, mutuality, triad effects, and a wide range of other structural features
- Obtain maximum-likehood estimates for the parameters of the specified model
- Test individual coefficients, assess models for convergence and goodness-of-fit – Simulate new networks from the underlying probability distribution implied by the fitted model
Prerequisites
- Basic concepts of statistics (mean, standard deviation, probability distribution)
- Basic concepts of network analysis (nodes, edges, degree, transitivity)
- Basic familiarity with R (network and sna packages)
References
1. Anderson, C.J., Wasserman, S., Crouch, B.: A p* primer: Logit models for social networks. Social networks 21(1) (1999) 37–66
2. Robins, G., Pattison, P., Kalish, Y., Lusher, D.: An introduction to exponential random graph (p*) models for social networks. Social networks 29(2) (2007) 173– 191
3. Robins, G., Snijders, T., Wang, P., Handcock, M., Pattison, P.: Recent developments in exponential random graph (p*) models for social networks. Social networks 29(2) (2007) 192–215
4. Goodreau, S.M., Kitts, J.A., Morris, M.: Birds of a feather, or friend of a friend? using exponential random graph models to investigate adolescent social networks. Demography 46(1) (2009) 103–125
5. Grund, T.U., Densley, J.A.: Ethnic homophily and triad closure: Mapping internal gang structure using exponential random graph models. Journal of Contemporary Criminal Justice 31(3) (2015) 354–370
6. Brughmans, T., Keay, S., Earl, G.: Introducing exponential random graph models for visibility networks. Journal of Archaeological Science 49 (2014) 442–454 7. Breure, A.S., Heiberger, R.H.: Reconstructing science networks from the past. Journal of Historical Network Research 3(1) (2019) 92–117
From historical source to network data
Claire Lemercier (CNRS, Paris)
This workshop is primarily aimed at complete beginners (there is no pre-requisite in terms of knowledge of network analysis methods); but it might also be interesting for practitioners of network analysis who are interested in making the most out of historical sources. Claire Lemercier will offer two short (ca. 10 minutes) lectures and lead a collective discussion/experimentation in the creation of network data from several different historical sources.
Lecture 1 will offer a tour of the wide range of historical sources that lend themselves to network analysis, and list principles of source criticism that are important to keep in mind when using each type of source
Lecture 2 will offer practical advice for the building of network data that stays as true to the source as possible and offers the best potential for network analysis (this lecture could be subtitled „against data cleaning“)
Most of the workshop will be devoted to a collective discussion based on a few examples of sources: the participants will collectively decide which kinds of ties between which kinds of nodes could be extracted from those sources, and how best to do it
Preparation:
If some registered participants would like a few pages from one of their sources to be one of the materials used in the collective discussion, they should send the sample pages to Claire Lemercier on 23 June at the latest. The source can be in any language but, for languages other than modern English, French, German, Spanish, or Italian, the participant should also send a short explanation of the contents.
As another optional preparation, participants are invited to consult the following texts:
For Lecture 1: Claire Lemercier, „Historical and archaeological network data„, in Tom Brughmans, Barbara J. Mills, Jessica L. Munson et Matthew A. Peeples (eds.), Oxford Handbook of Archaeological Network Research, Oxford, Oxford University Press, forthcoming (2021).
For Lecture 2: Marten Düring, „From Hermeneutics to Data to Networks: Data Extraction and Network Visualization of Historical Sources,“ The Programming Historian 4 (2015).
Introduction to Social Network Analysis: Basics and Historical Specificities

This workshop, intended for a beginner audience, proposes to review the main concepts of social network analysis (terminology, visual analysis, centrality measures, communities, etc.) while highlighting the challenges that arise when analyzing relational historical objects.
After an introduction to the basics of network analysis, we will provide an overview of the application of these methods in the historical sciences: there is no single way to extract a network from historical sources and this has implications for the types of analysis that can be done, sometimes creating biases that we must be aware of. And what is generally the status of network analysis in such research, is it a heuristic tool or just an illustration?
We will then look at the question of „translating“ the concepts and results of network analysis into a historical research. For example: how should betweenness centrality be interpreted? should community detection be used? can I trust the clusters that appear in the visual analysis?
To conclude, we will propose some reflections on the main difficulties of historical network analysis, between temporality analysis and multilevel system modeling.